La mécanique des fluides est une branche essentielle de la physique qui étudie le comportement des fluides, qu’ils soient liquides ou gaz. Cette discipline joue un rôle crucial dans divers domaines tels que l’ingénierie, l’aéronautique et l’hydraulique. En comprenant les principes de la mécanique des fluides, on peut mieux concevoir des systèmes et des équipements qui utilisent ou manipulent des fluides. Cet article explore les concepts fondamentaux de la mécanique des fluides, ses principales équations et ses applications pratiques.
Concepts Fondamentaux
La mécanique des fluides repose sur plusieurs concepts clés :
- Fluides : Les fluides sont des substances qui se déforment continuellement sous l’effet d’une force, qu’ils soient liquides ou gaz. Contrairement aux solides, les fluides ne conservent pas leur forme et s’écoulent pour remplir les espaces disponibles.
- Pression : La pression est une force exercée par unité de surface. Dans un fluide, la pression varie en fonction de la profondeur et de la hauteur par rapport au niveau de référence. La loi de Pascal stipule que la pression exercée sur un fluide incompressible se transmet de manière égale dans toutes les directions.
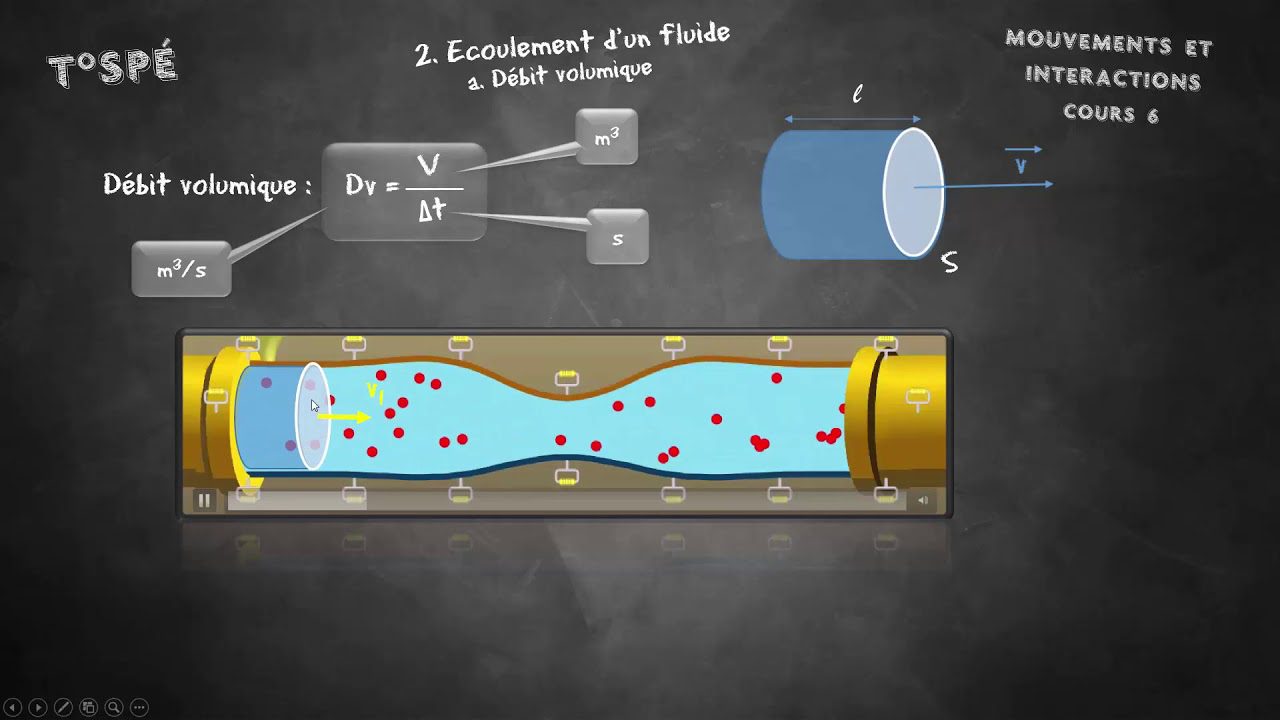
- Débit : Le débit mesure le volume de fluide qui passe à travers une section transversale par unité de temps. Il peut être influencé par la vitesse d’écoulement et la surface de la section traversée.
- Viscosité : La viscosité est une mesure de la résistance d’un fluide à l’écoulement. Elle joue un rôle crucial dans la détermination de la façon dont les fluides se déplacent et interagissent avec leur environnement.
Principales Équations de la Mécanique des Fluides
Plusieurs équations fondamentales régissent le comportement des fluides :
- Équation de Bernoulli : Cette équation exprime la conservation de l’énergie le long d’une ligne de courant dans un fluide en écoulement. Elle relie la pression, la vitesse et la hauteur d’un fluide, soulignant que la somme de l’énergie cinétique, de l’énergie potentielle et de l’énergie de pression reste constante.
- Équation de Navier-Stokes : Cette équation décrit le mouvement des fluides visqueux. Elle prend en compte la viscosité du fluide et les forces de pression pour prédire le comportement des fluides dans diverses situations, telles que les turbulences et les écoulements complexes.
- Équation de la Continuité : Cette équation exprime la conservation de la masse dans un fluide en écoulement. Elle stipule que le débit d’un fluide reste constant le long d’une ligne de courant, ce qui implique que le produit de la vitesse et de la section transversale est constant.
Applications Pratiques
La mécanique des fluides trouve des applications dans divers domaines :
- Ingénierie : Dans la conception de systèmes de plomberie, de pompes et de turbines, la compréhension des principes de la mécanique des fluides est essentielle pour garantir une performance efficace et fiable.
- Aéronautique : Les principes de la mécanique des fluides sont appliqués pour concevoir des avions et des hélicoptères, en étudiant l’aérodynamique pour optimiser la portance et la traînée.
- Hydraulique : La mécanique des fluides est utilisée pour concevoir et analyser des systèmes de gestion des eaux, tels que les barrages, les canalisations et les stations de traitement des eaux.
- Médecine : En physiologie et en médecine, la mécanique des fluides est importante pour comprendre le flux sanguin et les dynamiques des fluides corporels.
Conclusion
La mécanique des fluides est une discipline fondamentale qui influence de nombreux aspects de la technologie et de la science moderne. En comprenant les concepts clés tels que la pression, la viscosité et le débit, ainsi que les équations qui régissent le comportement des fluides, nous pouvons mieux concevoir des systèmes et résoudre des problèmes dans divers domaines. Que ce soit pour des applications industrielles, scientifiques ou médicales, la mécanique des fluides joue un rôle crucial dans notre compréhension du monde qui nous entoure.